W naszym potocznym rozumieniu chaos to coÂś niedobrego; coÂś, na co raczej nie czekamy - wiĂŞcej: przeraÂża nas myÂśl o spoÂłecznym chaosie, o chaotycznie pracujÂącej elektrowni atomowej itd. ChcielibyÂśmy mieĂŚ Âświat i wyobraÂżenie o nim uporzÂądkowane, staÂłe i niezmienne.
Lecz dzisiaj tego typu "jednoznaczne" teoria, zaÂłoÂżenia i wynikajÂące zeĂą "pewniki" zostajÂą bardzo powaÂżnie poddane w wÂątpliwoœÌ. PowĂłd? PrzemoÂżny wpÂływ (naturalnie nie zawsze przecieÂż uÂświadamiany) Teorii Chaosu. Dzisiejsza nauka, zwana teÂż „nowÂą naukÂą”, odchodzi i przekracza dotychczasowÂą wiedzĂŞ wraz z jej tradycyjnymi aksjomatami i porusza siĂŞ po obszarach, ktĂłre laikowi wydawaĂŚ siĂŞ muszÂą "paranormalne". Naukowcy teÂż majÂą swe przekonania, lecz trudno je nazwaĂŚ wiarÂą - trudno w coÂś wierzyĂŚ, gdy siĂŞ to wie... Teoria Chaosu - ktĂłra opiera siĂŞ na zaÂłoÂżeniu, iÂż moÂżliwe jest dokonywanie pomiarĂłw, kontrolowanie lub odtwarzanie matematycznie nieprzewidywalnego zachowania siĂŞ ukÂładĂłw lub przebiegu zjawisk (procesy chaotyczne moÂżna zaobserwowaĂŚ np. w przebiegu zjawisk atmosferycznych bÂądÂź w turbulencjach ruchliwych cieczy, kiedy to ledwie dostrzegalne zak³ócenia warunkĂłw poczÂątkowych powodujÂą znaczÂące zmiany w koĂącowych stadiach ruchu; istnieje poetyczna wizja motylego skrzydÂła, ktĂłre wprawione w ruch w Afryce wpÂływa na przebieg globalnych zjawisk klimatycznych) - po prostu dezaktualizuje wiĂŞkszoœÌ naszych dotychczasowych poglÂądĂłw, przekonaĂą i tradycyjnych wiar zbudowanych na starych paradygmatach, zupeÂłnie nieprzystawalnych jako narzĂŞdzia do dzisiejszych problemĂłw, potrzeb, pytaĂą i odkryĂŚ.
Dlaczego tak siê dzieje? Co siê sta³o? Otó¿ "odpowiedzialne" s¹ tu pospo³u: fizyka kwantowa, relatywizm nauki, zasada nieokreœlonoœci Wernera Heisenberga (teoria mówi¹ca, i¿ obserwacja danego procesu nieuchronnie oddzia³uje na ten proces, a zatem wyniki takiej obserwacji s¹ zawsze wartoœciami relatywnymi, nie absolutnymi), zasada antropiczna (zespó³ teorii fizycznych i kosmologicznych g³osz¹cych, ¿e obecnoœÌ cz³owieka (gr. anthropos) we wszechœwiecie nie jest przypadkowa, a cz³owiek jako obserwator kosmosu jest czynnikiem determinuj¹cym prawdopodobieùstwo w fizyce, ma on te¿ zasadniczy wp³yw na powstawanie rozmaitych zjawisk we wszechœwiecie, przetwarza i przekazuje informacje, co by³oby potwierdzeniem Einsteinowskiej koncepcji czasoprzestrzeni), a tak¿e wynikaj¹ca z tego wszystkiego "nowa kosmologia".
Dokonuj¹c analizy wy³¹cznie na bazie fizyki (szczególnie dynamiki) rozró¿niamy trzy mo¿liwe typy zachowaù uk³adów dynamicznych: periodyczne (w³¹czaj¹c tu niezale¿ne od czasu), quasiperiodyczne i chaotyczne. Zachowanie quasiperiodyczne jest z³o¿eniem przebiegów periodycznych o niewspó³miernych czêstoœciach.
Zachowanie chaotyczne charakteryzuje siĂŞ niestabilnoÂściÂą (brakiem stanu rĂłwnowagi, nie trwaÂłoÂściÂą) rozwiÂązaĂą rĂłwnania ruchu ze wzglĂŞdu na warunki poczÂątkowe. Oznacza to, Âże dowolnie maÂła zmiana stanu poczÂątkowego prowadzi po jakimÂś czasie do jakoÂściowych zmian trajektorii.
Chaos nie wystĂŞpuje w ukÂładach, opisanych liniowymi rĂłwnaniami ruchu.
Do analizy ukÂładu wykazujÂącego charakter chaotyczny uÂżywa siĂŞ specjalnie do tego zdefiniowanych pojĂŞĂŚ. PowyÂżej wspomniaÂłem o „czasie charakterystycznym”. Có¿ to takiego? UkÂład chaotyczny jak wiemy wzmacnia odchylenia poczÂątkowe, wiĂŞc czas charakterystyczny ukÂładu jest okresem po ktĂłrym odchylenie to wzrasta dziesiĂŞciokrotnie. Dwie trajektoria odlegÂłe na poczÂątku o d bĂŞdĂŞ po upÂływie czasu charakterystycznego odlegÂłe o 10d. Drugim waÂżnym pojĂŞciem jest atraktor. Definiuje siĂŞ go jako wyró¿niony podzbiĂłr moÂżliwych stanĂłw ukÂładu do ktĂłrego nieuchronnie zmierza ewolucja ukÂładu. Najlepiej jednak to przestawiĂŚ na przykÂładzie. MajÂąc do dyspozycji wahadÂło, mocujemy je i puszczamy z dowolnego poÂłoÂżenia. Wiemy, Âże pod wpÂływem siÂł tarcia (wahadÂło o powietrze oraz w zamocowaniu) zatrzyma siĂŞ w koĂącu po jakimÂś trudno przewidywalnym czasie. Wiadomo rĂłwnieÂż, Âże ten stan jest nieunikniony tj. osiÂągniĂŞcie w/w stanu nie jest zdeterminowane prĂŞdkoÂściÂą poczÂątkowÂą ani wartoÂściÂą wychylenia. Tak, wiĂŞc to spoczynkowe poÂłoÂżenie wahadÂła bĂŞdzie dla tego ukÂładu atraktorem. W powyÂższym przykÂładzie atraktorem bĂŞdzie konkretny punkt spoczynkowy jednak bardzo czĂŞsto spotyka siĂŞ, Âże atraktory o skomplikowanej strukturze. SzczegĂłlnÂą klasĂŞ stanowiÂą atraktory dziwne. OdwoÂłujÂąc siĂŞ do trajektorii moÂżna je zdefiniowaĂŚ jako takie, ktĂłre przyciÂągajÂą trajektorie z zewnÂątrz a ruch w ich wnĂŞtrzu jest chaotyczny i nieprzewidywalny. Bardzo sÂławnym atraktorem rozbudzajÂącym wyobraÂźniĂŞ naukowcĂłw od 1963r. (data publikacji) jest atraktor Lorenza. Jak juÂż wczeÂśniej wspomniaÂłem zajmowaÂł on siĂŞ metrologiÂą i postĂŞpujÂąc z duchem teorii chaosu udaÂło mu siĂŞ uproÂściĂŚ bardzo skomplikowane rĂłwnania opisujÂące zaleÂżnoÂści bardzo duÂżej liczby zmiennych. Wynikiem jego prac sÂą (sÂławne juÂż) trzy rĂłwnania ró¿niczkowe (juÂż wspomniane). Pomimo, Âże bazÂą byÂły badania metrologiczne same rĂłwnania przez znaczne uproszczenie uzyskaÂły pewien dystans od pierwotnych zaÂłoÂżeĂą. Tym nie mniej pozwoliÂło to zobrazowaĂŚ atraktor juÂż na pÂłaszczyÂźnie trzy wymiarowej.

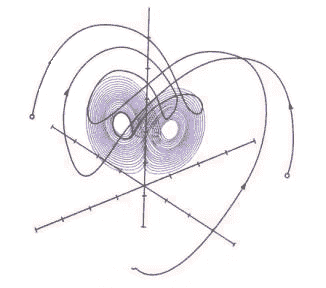
Poza „dziwnymi atraktorami” wystĂŞpujÂą teÂż atraktory samopodobne. W nich natomiast ksztaÂłty stajÂą siĂŞ bardzo uporzÂądkowane i systematyczne. DoskonaÂłymi przykÂładami sÂą fraktale.
Fraktalami (Âłac. fractus zÂłamany) nazywamy zbiory geometryczne, dla ktĂłrych wymiar jest liczbÂą naturalnÂą. PrzykÂładowo, fraktalem o wymiarze rĂłwnym stosunkowi logarytmu z 2 do logarytmu z 3 jest zbiĂłr Cantora (podzbiĂłr odcinka o wymiarze 1), a dywan Sierpinskiego (podzbiĂłr kwadratu) stanowi fraktal o wymiarze ln8/ln3.
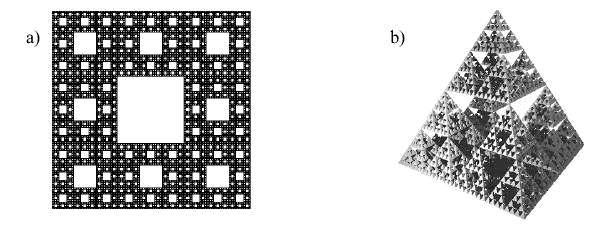
a) dywan SierpiĂąskiego o wymiarze D = ln8/ln3; b) piramida SierpiĂąskiego o wymiarze D = 2
WiĂŞcej znajdziesz tu:
http://www.fizykon.org/fiz_wspolczesna/teoria_chaosu.htm